topological subsytem codes: Pauli case

Quantum error correction techniques are central in quantum technologies. They allow for the supression of noise on the physical system, thereby extending the lifetime of encoded information. Unfortunately, the quantum error correction procedures can introduce additional faults.

Real-world applications of quantum error correction will have to deal with faulty measurement devices. This means that when the error syndrome is read out, it may not be correct. `Correction’ of the percieved syndrome may then result in introduction of additional errors.

One may attempt to negate the effects of measurement errors by repeating the syndrome measurements many times to gain confidence in the results [1]. Unfortunately, the number of measurement rounds typically scales with the code size. This leads to a large overhead in measurement time.

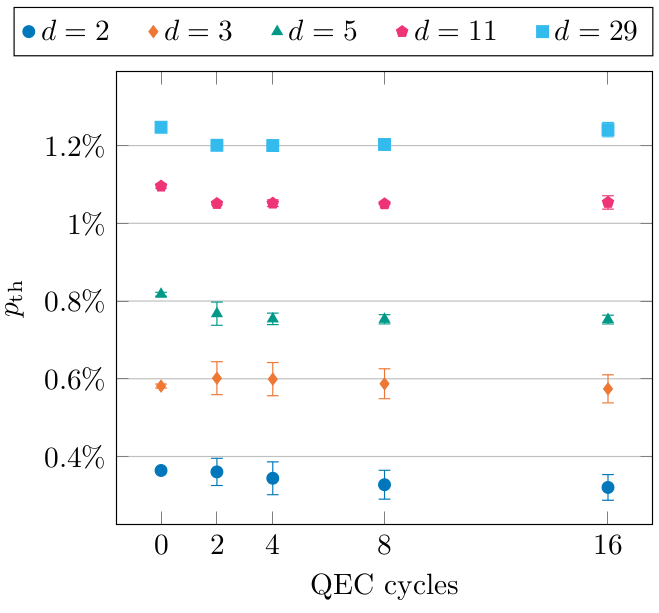
Topological subsystem codes [2,3] provide an alternative mechanism to mitigate measurement errors, via the property known as single-shot correctability. This allows for correction of the measurement errors with a constant number of measurement rounds.

In this work, we provide a new perspective on the subsystem Toric code of Ref. [3]. By focusing on the relations, rather than the stabilizer operators, we are able to provide a family of natural generalization. As input, these take 2-dimensional quantum double codes. From this perspective, the single-shot property arises from the topological order of the 2D code.

In addition, this perspective allows us to provide an argument that the most natural Hamiltonians associated to these 3D codes are gapless.

Threshold (clustering decoder) for the 3D \(\mathbb{Z}_d\) subsystem quantum double code under dephasing noise.